SPDC空间纠缠介绍

量子理论最显著的特征之一是纠缠，即量子系统显示出粒子或光子之间的非局域相关性，而这种相关性用经典物理学是无法解释的。例如，这可以通过违反贝尔不等式来证明。虽然在许多情况下讨论的是两级系统（量子比特）之间的纠缠，但多级系统之间的高维纠缠提供了更丰富的结构。

高维纠缠态具有吸引力，因为它们的信息容量更大，而且抗噪声和抗损耗能力更强。此外，利用自发参量下变频（SPDC）生成高维纠缠态以及利用液晶空间光调制器对其进行塑形也相对简单。

在 SPDC中，一束强平面波泵浦光束撞击非线性晶体，如 PPKTP（周期轮询 KTP）。在与晶体非线性系数相关的某种概率下，一个泵浦光子将被湮灭，同时产生两个纠缠光子（图 1a）。由于能量必须守恒，这两个光子的频率必须与泵浦光子的频率相加，这里我们将假设它们具有相同频率的退化情况（图 1b）。由于动量必须保持不变，因此产生的光子的波矢量必须与泵浦光子的波矢量相加，而泵浦光子的波矢量是指向特定方向的，因为泵浦光子是平面波。因此，这两个光子的横向动量将具有反相关性（图 1c）。这意味着，如果一个光子以某个角度发射，它的孪生光子就会以与泵浦光束相反的方向发射。

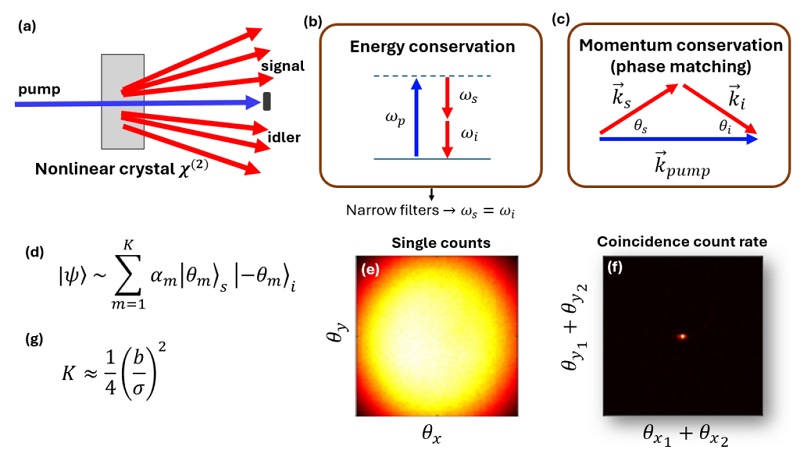
图 1： (a) 遵循能量（b）和动量（c）守恒的 SPDC 过程示意图。(d) 由此产生的量子态。(e)和(f)是大施密特数下晶体远场的典型单计数和重合计数。(g) 叠加态中的模式数的分析近似值。

事实上，这两个光子的生成状态是这些不同角度发射的相干叠加，每个光子的方向相反，其系数取决于精确的相位匹配条件（图 1d），通常像 sinc 函数一样取决于角度[5]。这些相关性可以在远场进行测量。使用简单的照相机，我们可以观察到 “单计数”，即在相位匹配允许的所有方向上发射的光子的平均强度，这可能是一个相当宽的区域（图 1e）。然而，如果进行重合测量，就会发现在某一角度测量到一个光子，那么孪生光子总是具有很强的相关性，并且会在更小的 “重合区域 ”中被发现（图 1f）。

重合区与单计数区之间的比率量化了量子叠加中不同模式的数量，这与其施密特秩有关[6, 7]（图 1g）。因此，要定制 SPDC 的空间纠缠特性，应同时考虑相位匹配函数的宽度（控制单计数区）和相关性的强度，并相应地规划光学装置。

具体来说，相位匹配 sinc 函数的角宽度 b，或等同于 SPDC 过程所允许的角度范围，由泵浦波长 λ_p 和晶体厚度 L 决定，约为 √(λ_p/L) 因此，虽然使用薄晶体会因相互作用长度较短而导致 SPDC 通量较小，但通常允许的发射角度范围较大，并会产生高度空间纠缠态。

相反，重合区域的宽度由泵浦的角频谱 σ 决定。事实上，对于具有单一定义明确的动量矢量的平面波泵浦来说，我们期待完美的相关性。然而，有限的泵浦光束必然包含许多不同的角度，这将导致动量守恒中的角度失配。这通常被称为从泵到 SPDC 相关性的角频谱转移。

总之，使用具有窄角谱的宽泵浦光束和薄晶体会增加 SPDC 空间纠缠的维度。关于有效模式数量的推理同样适用于近场： 宽泵浦光束会产生相应大的 SPDC 光子发射区域，而薄晶体则会导致每对光子在晶体输出端都具有很强的空间相关性，这是因为它们从产生点出发的传播距离很小。

当然，人们并不总是想要高维的空间纠缠。例如，在许多情况下，SPDC 光子会耦合到单模光纤中。在这种情况下，我们希望只产生一个空间模式，以获得与光纤的良好耦合。一个很好的经验法则是将泵浦的瑞利长度设定为晶体的长度。

相关产品：PPLN晶体、PPKTP晶体、SPPKTP晶体、PPLN晶体

详情链接：https://www.sinteclaser.com/optical/quantum-components.html