PPLN 晶体1560nm激光倍频过程的热效应分析

1 引言

780nm激光广泛应用于铷原子激光冷却与相关物理实验，而利用1560nm激光经过周期性化铌酸锂(PPLN)晶体倍频得到的780nm激光的方法也已经在此类实验中得到了应用。PPLN晶体由于有比较高的有效非线性系数和高阈值，在倍频实验中也得到广泛的使用，利用PPLN晶体倍频得到11.4W的780 nm的连续激光。在入射光功率不断增大的同时，晶体受激光加热的效果也就突显出来，热别是晶体处在长期连续工作状态下，这种热效应(TE)就不可避免。在倍频实验中发现，随着入射功率的增加，晶体需要的实际匹配温度反而下降，其实就是由于晶体的热效应引起。早在2002年就研究过PPLN倍频与温度之间的关系，并给出了倍频效率对应的温度带宽，从中可以看出倍频效率对温度的变化很敏感，可见温度在倍频实验中的重要性。目前主要是通过Ansys等有限元软件来计算仿真晶体热效应[8]，2010年，利用Ansys软件分析了高功率下磷酸钛氧钾(KTP)晶体的热效应，2011年，分析了PPLN的热效应对倍频效率的影响。本文介绍了准相位匹配与温度的关系，在此基础上，引入极化周期的受热膨胀对倍频的影响。通过Comsol有限元软件热学建模，精确地分析了激光穿过后晶体的温度分布，并深入研究了晶体尺寸、入射光束束腰半径、功率以及晶体散热方式对热效应的影响。

2 准相位匹配理论分析及其与温度之间的关系

2.1 准相位匹配及其与温度之间的关系

对于准相位匹配倍频过程，在小信号近似下，入射光为基模高斯光束时，非线性转换系数可以写成如下形式：

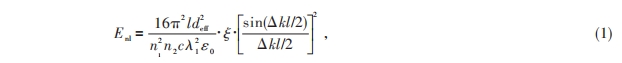
式中l为晶体长度，n1表示基频光的折射率，n2表示倍频光的折射率，c表示光速，λ1为基频光波长，ε0为真空介电常数，Δk=2k1-k2-Km，表示基频光与倍频光的相位匹配因子，k1和k2分别为基频光和倍频光波矢，Km=m∙2π/Λ,Λ为晶体的极化周期，m为准相位匹配的阶数，一般使用一阶，即m=1，非线性转换系数的单位为%/W，ξ=l/m为聚焦参数，表征高斯光束的聚焦和晶体长度之间的制约关系，当ξ=2.84时[12]有最优的束腰半径，deff=2d33/π,d33为PPLN晶体的有效非线性系数，这里的deff=17 pm/V。从(1)式可以看到，转换效率和晶体长度、光束的束腰半径等有关。

除此之外，Δk对非线性转换系数的影响很大，当Δk=0时，非线性转换效率达到最大，当Δk有一个偏移量时，倍频效率会快速地下降。

非线性转换系数中的折射率和温度直接相关，即ne(T,λ)，根据经验公式：

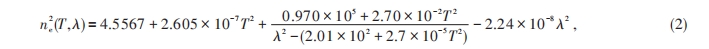
式中ne表示异常光的折射率，一般在准相位匹配中使用的是异常光，T表示晶体工作时的温度，单位为开尔文(K)，λ表示光波长，单位为纳米(nm)。

此时的相位匹配因子应表示为

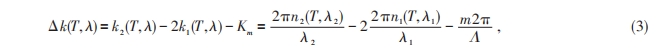
式中Λ为晶体的极化周期，m一般取一阶，即m=1，λ2为倍频光的波长，通过调谐晶体的工作温度T就可以使得Δk=0，即达到相位匹配。

2.考虑晶体极化周期受热膨胀下的温度分布

通过2.1节的分析可以看出，准相位匹配是通过调谐晶体的工作温度来实现相位匹配的。此时不得不考虑，晶体工作在匹配温度的时候，由于热胀冷缩，极化周期也会发生变化，又会影响晶体的匹配温度。铌酸锂晶体在0℃~600℃以内的热膨胀系数α=2×10-6 K-1，热膨胀方程为α=∂l/(l∙∂t)，可以得到极化周期与温度之间的关系，即Λ(T)=Λ∙exp[α(T-T0)]，其中，T0表示常温，取273.15 K。

此时非线性转换系数表达式也可以重新写成

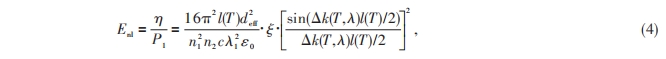
式中η=p₂/p₁,为转换效率 ,P1 和 P2 分别为入射光和出射光功率 。

通数值模拟，给出了晶体尺寸为1 mm×10 mm×40 mm,在入射光波长λ=1560.48 nm，极化周期Λ=19.2μm，考虑晶体的热膨胀效应时，非线性转换系数与温度的关系曲线如图1所示。

从图1中可以看出，在匹配温度附近，非线性转换效率对温度很敏感，当温度变化为0.5 K时，非线性转换系数就要降低50%，这也突出了分析晶体热效应的重要性；同时，考虑热膨胀效应后，非线性转换系数的分布并未发生明显变化，只是有一个整体平移的效果，图1中极化周期Λ=19.2μm时，匹配温度增加了0.38 K。

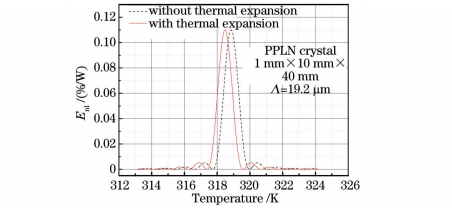
图1 非线性转换系数与温度的关系

除此之外，出射光功率的稳定性也是倍频过程中的一个重要指标，根据上述非线性转换效率和温度之间的关系，可以算出，当要求的功率抖动小于10 mW时，温度的抖动就必须要在1 mK范围以内，可见温度的抖动对倍频光功率的影响很大，对温控器件的要求当然也非常的高。

同时，通过数值计算，还给出了入射光波长λ=1560.48 nm，晶体长度l=40 mm时，实验中常用的几个极化周期在考虑和不考虑热膨胀效应的情况下，对应的匹配温度，如表1所示。

表1 不考虑热膨胀效应和考虑热膨胀效应时不同极化周期对应的匹配温度

由述的计算结果可以得出，考虑热膨胀对极化周期的影响时，晶体实际工作的匹配温度要高于不考虑时的匹配温度，而且随着极化周期的变短，这种热膨胀效应带来的匹配温度的修正也变得明显。这可能也是许多倍频实验未能取得和理论计算结果相近结果的一个原因，第3节中对于晶体的非线性转换系数的计算中均把热膨胀的影响考虑在内。

3 1560激光经过晶体的有限元分析

由第 2 节中理论分析可知，相位匹配要通过温度匹配来实现，同时非线性系数受温度变化的影响很大，那 么除了有热胀冷缩的影响外，还不得不考虑入射光对晶体的加热效果，称之为激光加热晶体的热效应 。

3.1 热学模型的建立和晶体的温度分布

当一束激光经过晶体的时候，会有部分的激光被晶体吸收。激光从入射端面照射入晶体后光强表达式为

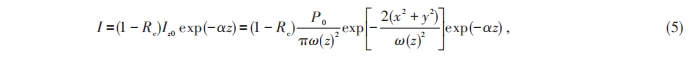
式中Rc表示入射端面的反射率，对于PPLN晶体，Rc=0.01，α为晶体对入射光的吸收系数，α=0.1%/cm，Iz0表示与传播方向垂直的入射端面上的光强分布，P0表示入射光功率，ω(z)表示z处的束腰半径，x，y是垂直z方向的横截面坐标。

光在入射晶体后，传播dz距离，就会有部分的光被吸收，即

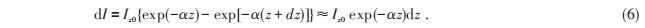
被吸收的光中部分转换为热能，所以体热源可以写成

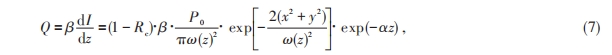
式中β表示转化为热能的光能占晶体吸收光能的比重，这里取30%，ω(z)在晶体长度的传输范围内可近似等于束腰半径ω0。

在常温下PPLN晶体的密度为4.64 g/cm3，导热系数为38 W/(m·K)，力学比热为630 J/(kg·K)。考虑到在实验中，晶体一直处在工作状态下，最终晶体的温度分布不会随时间变化，所以这个过程可以看作是上述体热源作用下的一个稳态热传导过程，则晶体内部的热传导遵守稳态热传导的Poisson方程为

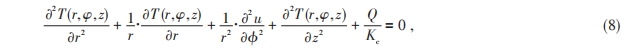
式中 T(r, φ,z) 为晶体中的温度场分布，Kc   为晶体的热传导系数，Q为晶体的体热源 。

上述的稳态热传导方程只有在一定的边界条件下才有解，结合实际实验中遇到的情况，晶体的入射端面和出射端面直接暴露在环境中，所以只与环境中的空气进行自然热对流交换。在这两个端面上可以用Newton冷却方程q=h(Ts-TL)来描述，其中，q表示热流密度，Ts晶体的温度，TL为环境空气的温度，h为对流交换系数，空气的热交换系数为3 W/m2 K。其他的4个面都被晶体夹具包裹，并连接有温控系统，在建立热学模型时，为了简单起见，可以认为其他的4个面也是和某种温度固定的流体进行热交换，只不过热交换系数和端面不一样，结合材料本身和实验中的实际情况，一般取h=150 W/m2 K。

对于上述方程的求解是通过有限元分析完成的，使用的软件是Comsol。几何模型为1 mm×10 mm×40 mm的长方体，材料的导热系数、密度和热容均按照晶体的属性来设定，并将晶体的外表面参数按照上述分析进行设置。取晶体的入射端面中心为坐标原点。因为晶体在工作前，温控系统会把晶体加热到匹配温度，所以在有限元仿真时，晶体的初始温度设置为匹配温度，与晶体出射端面和入射端面接触的环境温度设置为293.15 K，温控系统在工作时会将夹具稳定在匹配温度，所以除去端面的其他四个面的外界温度设置都为匹配温度。取晶体的极化周期Λ=19.2μm，此时的匹配温度T0=318.48 K，当入射光功率P0=30 W，束腰半径ω0=0.1μm时，可得到晶体总体的温度分布和出射端面的温度分布如图2所示。

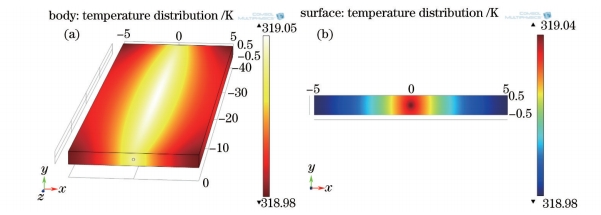
图2 温度分布 。 (a) 整个晶体; (b) 射端面

从图2可以看出，经过激光加热，晶体整体的温度被提高了0.5 K，且分布不均匀，激光穿过的部分，温度被提高了0.57 K。在晶体的入射断面和出射端面上，温度的分布同样也不均匀，光束中心的温度最高，达到319.04 K，离中心越远，温度越低，图3(a)为出射端面上y=0，温度沿着宽度(x轴)的分布，图3(b)为出射端面上x=0，温度在y方向的分布。可以看出温度沿着x或y方向成对称分布，但温度分布在x方向和y方向不一样，这是因为两个方向的尺度不一样，导致散热存在不同。除此之外，温度在z方向上也成类似的对称分布，如图3(c)所示，可以看到温度在晶体的中心达到最大，这是因为，随着激光穿过晶体，在z方向不断吸收热量，且在远离入射端面时，散热只能通过入射端面和与夹具接触的几个侧面完成，温度不断增加，到晶体中央时达到最大，但是过中央位置后，出射端面的散热也开始起作用，虽然仍然在吸收能量并转化为热量，但散热相比之前要大，所以在不断靠近出射端面的过程中，晶体的温度又开始下降，导致温度在轴向上呈现出以晶体中心线为对称轴的对称分布。

由于出射端面的温度存在一定的分布，必会导致非线性转换系数也存在着一定的分布，由3.1节的分析可知，温度提高0.5 K时，转换效率会下降一半，按照上述仿真结果，在入射功率P0=30 W并考虑热效应时，晶体的非线性效率会下降一半。可见在大功率情况下热效应对晶体的倍频效率影响显著。

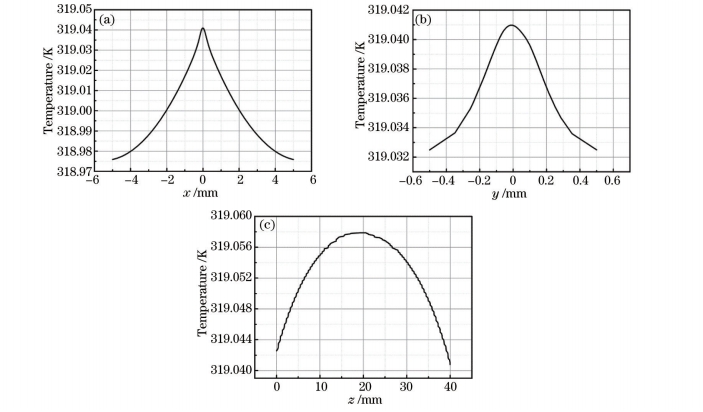
图3 出射端面(a) x 方向 、(b)  y 方向和 (c) 晶体轴向温度分布

3.2 考虑热效应时束腰半径内的温度场和非线性转换系数的分布

激光的倍频只发生在基频光与倍频光重合的位置，所以转换效率只有在两束光重合的位置才有意义。假设基频光与倍频光在倍频过程中始终在束腰半径位置内重合，这种假设也是比较合理的，因为在准相位匹配过程中，走离效应很小。此时可以看出，只有分析束腰半径内的温度分布对非线性系数的影响才有实际的意义，而这一点在其他分析非线性晶体热效应的文章中并未被指出，现在重点看一下晶体出射端面在束腰范围内的温度分布情况。同样取入射光功率P0=30 W，束腰半径w0=0.1 mm时，得到束腰半径内的三维温度分布如图4(a)所示，通过数值计算，得到在这种温度分布下，转换效率的分布情况如图4(b)所示。

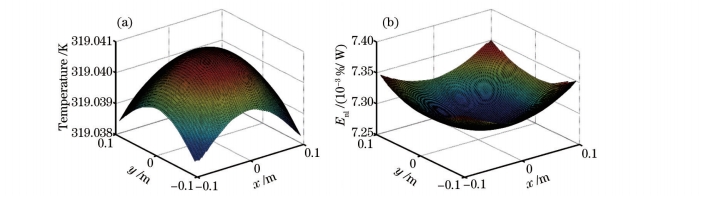
图4 束腰半径内的三维(a)温度分布和(b)非线性转换系数的分布

从计算结果可以看出，在束腰半径范围内，温度也呈不均匀分布，在束腰的中心位置温度达到最高，当远离中心时，温度会变低，束腰边界位置与中心的温度差有0.003 K，引起这样分布的一个很重要的原因是，入射光是基模的高斯光束。而这样的温度也足以引起转换效率的不同：从上述计算结果可以看出，在出射面的束腰半径内，非线性转换效率呈不均匀分布，束腰中心的非线性转换系数比边缘的低0.1%。

3.3 晶体长度对晶体热分布和非线性转换效率的影响

晶体的尺寸是影响倍频效率的一个很重要的参数，首先考虑晶体的长度，同样在入射光功率P0=30W，束腰半径w0=0.1mm，采用相同的纵向扫略方式的情况下，可计算出在不同晶体长度下，晶体出射端面中心的温度值如图5(a)所示 。

从图5(a)可以看出，随着晶体长度的增加，晶体整体的温度会有略微的上升，因为晶体长度的增加后，激光穿过晶体时，晶体吸收的总热量增加，但同时随着晶体长度的增加，散热面的面积也在增加，所以在长度继续变长时，温度的增加趋势趋于变缓。这对倍频过程是有利的，因为非线性转换系数随着晶体的长度增加而变大，而在长度增加的情况下，热效应带来的温度变化却不是很明显，对非线性转换系数的影响也较小。

温度随晶体宽度的变化如图5(b)所示，可以看出，晶体的温度随着宽度的增加而逐渐减小，这是因为晶体的主要散热是靠与夹具接触的上下面和侧面完成的，当晶体的宽度增加时，激光穿过晶体时被吸收的总热量并没有变化，但散热面却增加了，导致晶体的温度下降。在宽度到9mm以后，温度随晶体宽度的增加趋于缓慢。

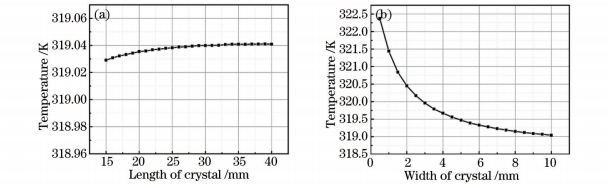
图5 晶体温度与晶体(a)长度和(b)宽度的关系

3.4 入射光功率对晶体的热分布的影响

在束腰半径ω0=0.1mm、晶体尺寸为1mm×10mm×40mm的情况下，通过改变入射光功率，得到晶体出射端面中心温度的变化，如图6(a)所示，在输入光功率为2~60W的范围内，温度和光功率之间成线性关系，光功率每增加1W，温度就会上升0.02K，这样的线性关系有利于推算不同入射功率时，晶体的温度上升情况。除此之外，还能看到，在不同功率入射的情况下，束腰半径内的温度分布的变化，以y方向的温度分布代替整个束腰的温度分布，从图6(b)可以看到，当入射功率变大，晶体整体温度提高的同时，晶体出射端面的温度差也在变大。而这种温度差的变大，必然会增大非线性转换系数在束腰范围内的不均匀性。

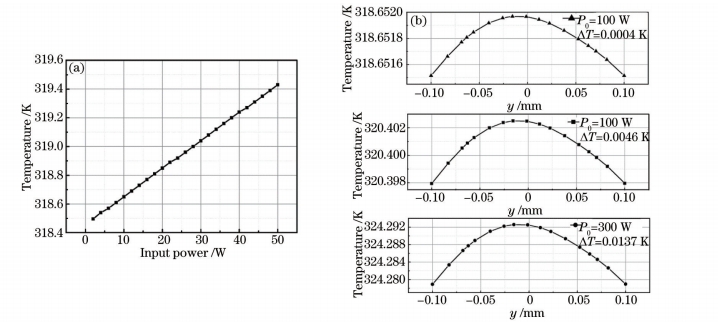
图6 (a) 晶体温度与入射光功率的关系; (b) 不同入射光功率下束腰范围内温度分布

3.5 晶体的散热方式对热分布和非线性转换效率的影响

常用的三种散热方式的入射端面和出射端面均直接和环境接触，通过与环境中空气的热对流进行散热。第一种散热方式是晶体的上顶面和两个侧面均被导热性较差的物质包裹以保持晶体的温度，底面连接控温器件。第二种散热方式是晶体的上表面被导热性较差的物质覆盖，两个侧面和底面连接控温器件。第三种散热方式是晶体的上下表面和两个侧面都和控温器件连接。这三种方式对应的其实是不同的晶体夹具。在入射光功率P0=30 W，束腰半径ω0=0.1μm，晶体尺寸为1mm×10mm×40mm的情况下，晶体在出射端面上x=0，y方向的温度分布如图7(a)所示。可以发现，在三种方式中，第一种散热方式下晶体的整体温度最高，第二种其次，第三种最小。这是因为就散热面而言，第一种散热方式的散热面最少，只有一个底面为主要的散热面，第二种方式有三个散热面，散热效果明显比第一种好很多，第三种方式有四个散热面，散热效果比前两种都要好。同时还可以看出，由于第一种方式只有一个底面散热，温度分布的对称性遭到破坏，同样第二种也是因为有三个面散热，温度分布的对称性同样遭到了破坏，而且分布情况和第一种相反，因为和第一种情况相比，第二种的散热部分正好是第一种方式的不良导热部分，这两种散热方式都会使温度分布更加不均匀。第三种散热方式则比较理想，在y方向呈对称分布。综合上述的分析，在晶体散热的方式选择方面，应当选择第三种散热方式，即晶体的4个面都连接有散热效果的控温器件。

重点分析第三种散热方式中晶体与夹具接触4个面的散热情况，即表面换热系数对热效应的影响，取换热系数h为150、900、1500 W/(m2.K)分别对应铝、紫铜和涂抹导热硅脂的散热材料。得到输出端面内x=0，y方向上的温度分布，如图7(b)所示。

>由图7可以看出，传热系数越大，晶体整体的温度越低，但出射端面上的最高温度和最低温度的变化不大，即传热系数的大小并不会有效地改变晶体的温度分布情况。

因此，在考虑晶体的散热时，最好选用四面包围的散热方式和有比较好的散热特性的材料，如在控温器件与晶体之间涂抹导热硅脂等。

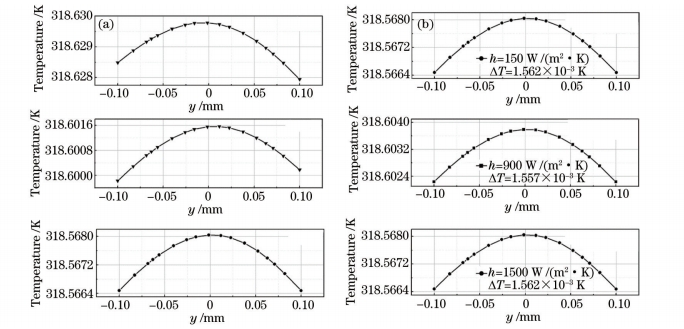
图7 (a) 不同散热方式对应的束腰范围内的温度分布; (b) 不同传热系数对应的束腰范围内的温度分布

4 结论

结合1560nm激光经PPLN晶体倍频至780nm的实例，精确计算了考虑晶体极化周期的热膨胀效应时非线性转换系数与温度之间的关系，发现考虑热膨胀时，晶体的匹配温度比没有考虑时要高，并指出非线性转换系数受温度变化的影响比较大。通过有限元计算得到在入射光功率P0=30 W，晶体尺寸为1mm×10mm×40mm，ω0=0.1mm情况下，倍频过程中晶体的三维热温度布和出射端面的温度分布，并分析计算了晶体尺寸、入射光束腰半径、入射光功率和三种不同散热方式对热效应的影响，得出如下结论：1)晶体的温度呈一定的对称分布，不均匀；2)晶体的长度对晶体温度增加的影响不明显，宽度影响较大，宽度越大，散热越好，在实验条件允许的情况下，选用宽的晶体有利于散热；3)入射光功率和温度成正比；4)使用良导热的材料包裹晶体的上下面和两个侧面的散热方式有利于晶体的散热，且能使晶体的温度分布更加均匀。

所做计算和分析对提高倍频实验的转换效率和研究晶体在倍频过程中的温度分布有一定的参考意义。